Por Jonas Tieppo da Rocha
A geometria de alguns componentes pode facilmente ser abstraída como uma casca, o que leva a assumir a hipótese de estado plano de tensões, fato que necessariamente simplifica consideravelmente a dimensão do problema.
No entanto, em algumas situações, por mais que a geometria seja pouca espessa, tal abordagem não é possível. Basicamente por duas razões:
- O engenheiro pode necessitar ver a distribuição de tensões detalhada na espessura – o Abaqus consegue plotar em algumas posições, porém uma análise tridimensional consegue fornecer detalhes como deformações cisalhantes fora do plano – que em geral são responsáveis por fenômenos como delaminação, em compósitos.
- O engenheiro pode estar analisando um material hiper elástico, cuja formulação já assume uma lei constitutiva tridimensional.
Como alternativa aos elementos tridimensionais lineares, o Abaqus possui o elemento denominada CSS8, o chamado Continuum solid shell element. Sua formulação possui 7 modos incompatíveis, que favorecem sua performance em flexão e evitam o empecilho do shear locking. O elemento é baseado no princípio variacional de Fraeijs de Veubeke–Hu–Washizu (FHW), cujo comportamento reproduz de forma satisfatória a flexão planar e fora do plano [1]. A seguir, vamos comparar os resultados obtidos por meio de três metodologias:
- Análise com elemento hexaédrico linear;
- Análise com o elemento CSS8 (Continuum solid shell);
- Análise com elemento de Casca.
Tais metodologias irão tentar descrever as tensões obtidas em uma placa engastada sob flexão, sobre uma pressão à face normal da placa. A vantagem de se usar o elemento CSS8 será grifada.
Resultados
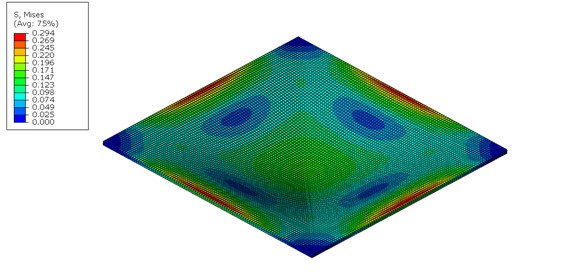
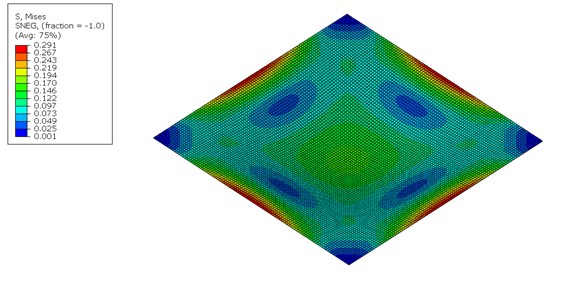
Primeiramente, vamos comparar as tensões de von Mises obtidas em cada situação.
Tensões de von Mises

Comentários
Pode-se ver que o modelo Solid Shell possui uma proximidade muito maior com o modelo de casca, ao se comparar a magnitude das tensões de von Mises, como ilustra-se nas figuras 1, 2 e 3. A formulação do Solid Shell consegue aferir as tensões de forma satisfatória utilizando apenas dois elementos na espessura, mesmo que não se utilize da hipótese de estado plano de tensões. A título de curiosidade, o engenheiro pode aferir as tensões na direção perpendicular, utilizando o modelo Solid Shel, como é ilustrado na figura 4. Nota-se que a magnitude das tensões em grande parte da região é nula, o que corrobora com a hipótese cinemática assumida pelo elemento de casca.

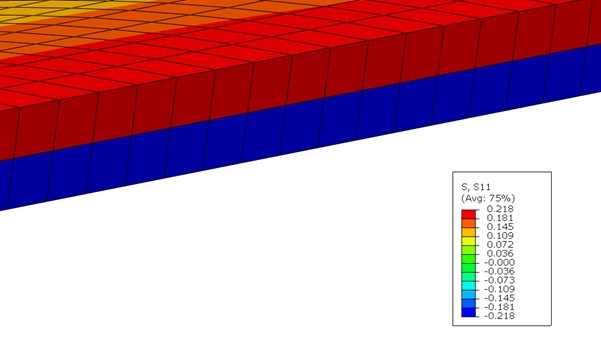
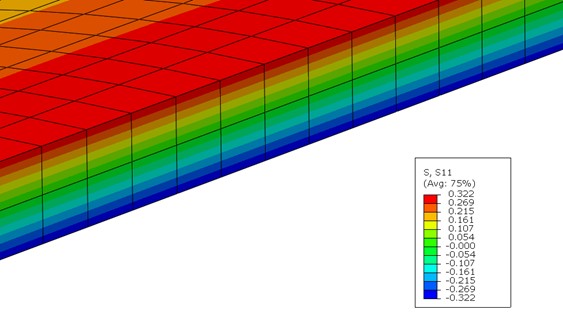
Tensões De flexão
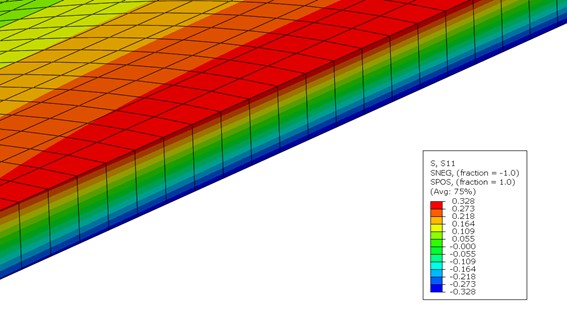
A seguir, mostra-se o resultado para as tensões de flexão. Como é esperado, o elemento sólido linear representa um comportamento não aceitável fisicamente, já que há um salto brusco de tensão entre os elementos superiores e inferiores (Figura 5). O elemento Solid Shell tem resultados congruentes com o elemento de casca, conseguindo descrever uma distribuição linear de tensão, compressiva nos elementos inferiores e trativa nos superiores (figuras 6 e 7).
Conclusão
Os resultados indicam que o elemento Solid Shell possui uma grande capacidade de descrever comportamento sobre flexão, superando a conhecida deficiência do elemento sólido de travamento ao cisalhamento. Portanto, nas situações em que a modelagem de geometrias planas exige elementos tridimensionais, recomenda-se o uso do elemento Solid Shell.
Referências
[1] Vu-Quoc, L., & Tan, X. G. (2003). Optimal solid shells for non-linear analyses of multilayer composites. I. Statics. Computer methods in applied mechanics and engineering, 192(9-10), 975-1016.




















